Returning to Fourier Transformations with Maxima
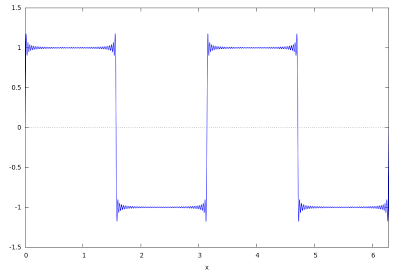
The last time that I worked with Fourier Transformations was in Linear Analysis, nearly 3 years ago. Now I am taking a class in Mechanical Vibrations, and we are returning to this theory. The other week, while learning to use a spectral analyzer, we had to derive the first 3 Fourier coefficients for a sine wave, square wave, and triangle wave. All of that aside, after lab I played around with some fourier theory in Maxima. Maxima Maxima is a symbolic math program (similar to Mathematica) that I ran into last quarter in order to supplement Octave (Matlab equivalent). Like Octave (which does only numerical analysis) Maxima is completely free. I like the version of Maxima called wxMaxima , and I have that installed on Ubuntu. You can define an equation in maxima such as: s: a^2 + 7 = b*4 + a/3 Then you can solve for b in one step: solve(s,b) And it simply returns b = a^2/4 + a/12 + 7/4. You can do other cool things such as summation, integration, ...